Das ist doch kein Zustand: Und und Oder, oder Nicht?

Die Phrase „Das ist doch kein Zustand!“ hat wohl sicher jede_r schon einmal gehört, der das Chaos liebt – in Wirklichkeit wissen wir aber (ich zähle mich zu den Chaoten): Diese „Zustände“ haben ihre eigene Ordnung – und wenn man die einmal durchschaut hat, ist der Umgang mit den Zuständen überhaupt nicht mehr umständlich!

Ähnliche Beiträge gibt es wahrscheinlich wie Sand am Meer – und viele davon sind auch echt weiterzuempfehlen, aber ich denke mir, dieser grundlegende Begriff hat auch in diesem Blog einen eigenen Beitrag verdient.

Es geht im Prinzip um alles, was es gibt – denn alles hat irgendeinen Zustand. Und darum, was den quantenphysikalischen Zustand von dem, was wir intuitiv darunter verstehen würden, unterscheidet.

Was man öfter mal hört ist die Frage: „Ist das noch in einem guten Zustand?“. Irgendwie scheint sie wichtig zu sein. Aber welche Antwort erwartet man sich darauf? Ein simples Ja wird wohl den einfachen Gemütern reichen, aber eigentlich möchte man gerne viel über das Ding, über dessen Zustand man rätselt, erfahren. Nennen wir dieses Ding einmal wie die Physiker_innen: System.

Es ist ein Ding in der realen Welt, und was reale Dinge so an sich haben, sind ihre Eigenschaften. Ohne besonders existenzialistisch zu werden: Was ist ein Ding ohne Eigenschaften? Ist sein simples Dasein nicht schon genug? Würde sich etwas ändern (z.B. irgendeine Form von Wirkung), wenn es nicht da wäre?

Wir erwarten uns auf diese Frage – ganz generell – Aussagen. Aussagen, die das Ding betreffen. Betrüger_innen z.B. können das, was wir erwarten, ganz gut ausnutzen. Logisch, oder? Da aber die ganze Welt irgendwo doch auf quantenphysikalischen Grundlagen fußt, stellt sich weiter die Frage: Ist das noch in einem guten quantenphysikalischen Zustand? Und hier fängt das Problem an – und es zieht sich durch. Eigentlich ist alles, was an der Quantenphysik seltsam ist, darauf zurückzuführen, dass es hier um Zustände geht, für die wir Menschen im Alltag kein Konzept – keine Begriffe und keine Intuition haben. Die Aussagen, die wir gewöhnlich über Dinge, die wir kennen, treffen, gehorchen einer bestimmten Logik (ganz passend dazu: Aussagenlogik). Das hört sich jetzt vielleicht zu mathematisch an, ist aber eigentlich nicht so schwer – und nicht einmal so streng (man muss hier keine Vulkanier beschwören).

Aussagen über den Zustand von Dingen können entweder manchmal wahr sein (wenn sie zutreffen), manchmal falsch sein (wenn sie nicht zutreffen), immer wahr sein oder immer falsch sein (das nennt man dann etwa eine Tautologie) – sie kann sich auch selbst widersprechen, wie z.B. diese „Diese Aussage ist falsch“. Davon wollen wir uns in der Physik zwar eher fern halten, aber im Alltag haben wir keine Probleme mit solchen Aussagen – sie sind irgendwie interessant, weil man lange darüber nachdenken kann.

Noch interessanter wird es aber mit Aussagen, die Mu sind. Wolfgang Pauli, ein österreichischer Quantenphysiker aus der Pionierzeit der Quantenmechanik, hat das Mu gut zusammengefasst: „Das ist nicht nur nicht richtig, es ist nicht einmal falsch!„

Das kann etwa passieren, wenn man die Alltagslogik (die Aussagenlogik) auf Dinge anwendet wie Quantenzustände, die zwar Zustände genannt werden, aber mit jenen klassischen Zuständen, die wir so intuitiv erfassen, nicht mehr viel zu tun haben. Die Quantenlogik ist aus dem Grund eine andere Logik als unsere klassische, weil die Dinge, die sie in ihren Aussagen miteinander in Beziehung setzt keine klassischen Zustände sind. Und klassische Zustände sind im Prinzip nichts weiter als Eigenschaften von Dingen, sogar deren „bloße“ Existenz.

Ein System ist immer in einem einzigen Zustand: Das ändert sich auch in der Quantenphysik nicht – nur was genau unter Zustand gemeint ist, ist äußerst unintuitiv. Ein System kann prinzipiell mehrere mögliche Zustände einnehmen, ist zu jedem Zeitpunkt aber immer nur in einem. Ich selbst etwa kann traurig sein – oder fröhlich. Ich kann auch traurig und fröhlich gleichzeitig sein – das ist aber noch nicht Quantenphysik: Gleichzeitig traurig und fröhlich zu sein ist einfach ein weiterer Zustand, in meinem Fall: ein Gemütszustand.

Wenn wir das alles ein bisschen vereinfachen wollen, dann nehmen wir doch einfach das – beinahe – einfachste System: Eines, das nur drei verschiedene Zustände annehmen kann (d.h. zu jedem Zeitpunkt ist es in einem von drei möglichen Zuständen): etwa ein dreiseitiger Würfel – hier ist ein bisschen Fantasie gefragt! (Noch einfacher wäre ein System, das nur zwei mögliche Zustände annehmen kann. Würfelt man, so zeigt der Würfel immer eine von den drei Seiten: Das ist sein Zustand. Die drei Seiten unseres Würfels nennen wir: Rot, Grün und Blau – diese Wörter sind willkürlich gewählte Bezeichnungen für die drei möglichen Zustände dieses Würfels.

Um Aussagen über den Würfel zu treffen, müssen wir nicht unbedingt mehr über ihn wissen. Eine gute Aussage wäre etwa:

Der Würfel ist Rot oder Grün oder Blau.

Diese Aussage ist sogar eine Tautologie – sie ist, mit unseren Annahmen, immer wahr.

Der Würfel ist Rot oder Grün.

Wenn diese Aussage wahr ist, wissen wir schon ein bisschen mehr. Außerdem sehen wir hier intuitiv, was das Oder bedeuten soll: Der Würfel ist entweder Rot oder Grün, aber nicht beides. Das ist das exklusive Oder, das Entweder-Oder, das in der Alltagssprache dominiert, das wir gewöhnlich meinen, wenn wird „oder“ sagen.

Es gibt auch ein inklusives Oder, was soviel bedeutet wie: Entweder eines von beiden oder beides. Das verwendet man nicht so wirklich, hat aber seine Berechtigung. Die Aussage: Ich bin glücklich oder traurig interpretieren wir normalerweise nicht als: „Entweder ich bin glücklich oder ich bin traurig oder ich bin beides gleichzeitig“.

Das Und und das Nicht kommen in solchen klassischen Aussagen auch oft vor:

Der Würfel ist nicht Grün und nicht Blau.

Hier können wir sogar logisch schlussfolgern: Der Würfel ist rot – diese Aussagen sind äquivalent. Vorausgesetzt, niemand belügt uns. Das Und ist klassisch immer inklusiv: Macht es sind zu sagen, ich bin fröhlich und traurig, wenn ich damit nur eines von beiden meine?

Was in der Quantenphysik bis jetzt übrig bleiben würde: Wenn wir einen Quantenwürfel anschauen würden, würden wir ebenfalls immer einen dieser Zustände sehen. Bloß: In der Quantenphysik hätte der Würfel noch unendlich viele andere.

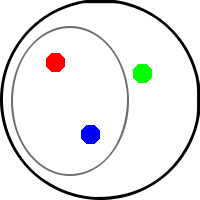
Unsere klassische Logik und damit unser Denken lässt sich im Prinzip durch die Mengenlehre mathematisch beschreiben – in dieser Sichtweise ist sie besonders intuitiv: Man kann Aussagen aufzeichnen. Das macht man, in dem man alle möglichen Zustände in einen (imaginären) Sack wirft und dann – für die verschiedenen Aussagen, ob sie jetzt wahr sind oder nicht, kleine Kreise zeichnet:

Im kleinen grauen Kreis ist die Aussage „Der Würfel ist nicht Grün“ visuell dargestellt.

Analog dazu gibt es Regeln, die eine Interpretation von Und und Oder ermöglichen:

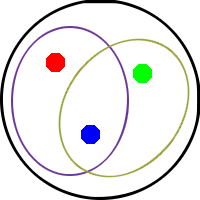
Der lila Kreis stellt die Aussage „Der Würfel ist nicht Grün“ dar (also sind Rot und Blau eingekreist), der gelbliche Kreis die Aussage „Der Würfel ist nicht Rot“ (also sind Grün und Blau eingekreist).

Verknüpfen wir die beiden Aussagen mit einem Und, zuerst verbal: „Der Würfel ist nicht Grün und der Würfel ist nicht Rot“, dann reden wir über die Schnittmenge der beiden bunten Kreise – Blau: Jene Farbe, die in beiden Kreisen gleichzeitig vorkommt.

Verknüpfen wir die Aussagen mit dem inklusiven Oder, dann erhalten wir: „Der Würfel ist nicht Grün oder der Würfel ist nicht Blau oder er ist beides nicht“, dann erhalten wir – in diesem Fall – eine Tautologie (der Würfel ist immer entweder nicht Grün oder nicht Rot).

Im Allgemeinen kann man das inklusive Oder als die sogenannte Vereinigungsmenge darstellen. Das wären die Zustände, die mindestens in einem der Kreise (in einer der Aussagen) vorkommen, aber auch in mehreren gleichzeitig vorkommen könnten.

Das exklusive Oder enthält die Zustände der Vereinigungsmenge ohne die Zustände der Schnittmenge: also jene Zustände, die in einer der Aussagen oder der anderen vorkommt und nicht in beiden. Das exklusive Oder ist also einfach eine Verbindung aus dem inklusiven Oder und einem Und-nicht.

In der Quantenphysik funktionieren diese Kreiszeichnungen nicht mehr, und das ist sogar schon nachgemessen worden: Mithilfe der Bellschen Ungleichung (bell’s theorem). Die Bellsche Ungleichung ist nicht schwer zu verstehen: Immer, wenn es um etwas geht, dass der klassischen Logik entspricht, man es also in diesen Diagrammen aufzeichnen kann, dann trifft sie zu.

Für quantenphysikalische Systeme hat man allerdings festgestellt: Die Bellsche Ungleichung ist verletzt – man kann Aussagen in der Quantenphysik nicht in solchen Diagrammen darstellen. Das heißt: Wir können nicht darüber reden, ohne dass uns der Kopf dabei wehtut. Intuitiv gesagt, aber wohl sehr abstrakt, gibt es in der Quantenphysik so etwas wie ein exklusives Und.

Der Grund dafür: Zustände von quantenphysikalischen Dingen lassen sich nicht in den Sack der Mengenlehre packen, um zu klassischen Aussagen über sie zu kommen. Auch nicht in eine überabzählbare Menge, aber das ist eine andere Geschichte.

Wie lässt sich dann ein quantenphysikalischer Zustand überhaupt begreifen? Das heißt: Wie soll man mit ihm umgehen?

Easy – aber abstrakt.

Wir gehen immer noch von einem, quantenphysikalischen, Würfel aus, der einem eine von drei Farben zeigt, wenn man denn hinschaut. Zuerst einigt man sich dann auf eine Bezeichnung einiger möglicher quantenphysikalischen Zustände – Rot, Grün und Blau sind OK. Das sind meistens die Zustände, die man eindeutig voneinander unterscheiden kann. Allerdings packt man sie zwischen lustige Striche:

.

Ganz kurz kann man so ein Ding einen ket nennen (oder einen Ket-Vektor). Das liegt daran, dass es auch noch den bra gibt, und zusammen sind sie: bra-kets: Jeder bra hat seinen ket:

Die Striche haben nichts besonderes zu bedeuten, außer als Signal: Achtung, das ist ein quantenphysikalischer Zustand! Gemeinsam sind bras und kets eine sehr einfache und trotzdem wirklich mächtige Weise, quantenphysikalische Dinge symbolisch darzustellen (it’s a really good notation). Es gibt natürlich einige Regeln, wie man mit diesen Zuständen umgeht – analog zu den Regeln mit den Kreisen und welche Aussagen durch welche Kreise dargestellt werden können.

Neu ist: Wenn wir uns auf diese drei Zustände unseres Quantenwürfels geeinigt haben, dann gibt es noch viel, viel mehr Zustände – Kombinationen aus den anderen Zuständen, die aber nicht dasselbe sind wie die Kombination aus „fröhlich“ und „traurig“ weiter oben, sondern eher – intuitiv – durch ein exklusives Und verbunden sind (was es eigentlich nicht gibt).

Man darf nämlich einen Quantenzustand (quantum state)  auch mit Zahlen multiplizieren und erhält dann einen weiteren, gültigen Quantenzustand. Die Zahlen, mit denen man multipliziert, müssen zwar bestimmte Voraussetzungen erfüllen, und sind nicht ganz so intuitiv (es sind nämlich komplexe Zahlen), aber in der Quantenphysik gibt es noch viel schlimmere Zahlen (Grassmann-Zahlen), das ignorieren wir hier aber erstmal. Man macht das natürlich nicht zum Spaß – es wird sich herausstellen (nicht hier und heute), dass diese Zahlen eine sehr (nicht ganz) reale Bedeutung haben.

Man kann zwei Zustände addieren (das ist besser formuliert als „exklusives Und“) – und erhält einen weiteren, normalen Zustand, in dem sich der Quantenwürfel befinden kann:

Und: dieser Zustand ist nicht „Gelb“, den gibt es nämlich nicht, wenn man hinschaut sieht man auch nicht Rot und Grün gleichzeitig (das wäre ja wieder unser inklusives Und). Wir haben ja doch gesagt, es gibt nur drei Zustände, wenn wir hinschauen! Aber was bedeutet dieses „Addieren“? Mann könnte sagen: Der Quantenwürfel ist Rot plus Grün, was dasselbe ist wie Grün plus Rot: In Wirklichkeit bedeutet „Addieren“ hier nämlich nur, dass das, was man in der Schule über Addition gelernt hat, hier getrost angewendet werden kann. Also, dass dasselbe ist wie – keine Selbstverständlichkeit! Rot plus Grün ist also ein neuer Zustand, und das heißt, er ist ein weiterer ket.

Man sieht sehr schön, dass es in unsere Köpfe nicht konkret hineinwill: Was heißt, dass ein Quantenwürfel Grün plus Rot ist, womöglich auch noch: Vier mal Grün plus acht mal Rot? Wie sieht das aus? Naja, die Antwort lautet: entweder Grün oder Rot oder Blau – wenn man hinschaut. Und was ist der Zustand des Quantenwürfels, nachdem man hingeschaut hat?

Das heißt: Wenn man danach noch ein zweites Mal hinschaut, wird man dieselbe Farbe sehen wie zuvor (wenn dazwischen nichts besonderes passiert ist). Was hier wirklich wichtig ist: Der Zustand ist nicht unbedingt das, was man auch sieht, aber wenn man einmal hingeschaut hat, ist der Würfel in dem Zustand, den man zuvor beobachtet hat. Man kann sich vorstellen, dass man, um das darzustellen, auch Regeln braucht, die einem sagen, wie man „Beobachtungen“ aufschreibt.

Außerdem haben Zustände eine Art Länge. Die erhält man, wenn man einen bra mit seinem ket „multipliziert“ (dabei gibt es etwas andere Regeln als bei der gewohnten Multipikation) – dabei kommt eine Zahl heraus, deren Wurzel eine Art von Länge darstellt. Was misst diese Länge? Ganz knapp: Sie misst, wie ähnlich sich zwei Zustände sind!

Meistens macht es Sinn, um verständliche Antworten auf eine Frage zu bekommen, die Länge aller Zustände – willkürlich – auf „1“ (Eins) zu setzen – das geht leicht, weil man einen Zustand ja mit beliebigen Zahlen multiplizieren kann. Falls ein  Zustand also doppelt so lang ist, wie er sein sollte, dividiert man ihn einfach durch Zwei. Auf die Länge kommt es in der Quantenphysik nämlich eigentlich nicht an.

Kürzen wir ab jetzt die Zustände Rot, Grün und Blau mit R, G und B ab. Formal schreibt man dann:

Das macht man, weil man auf die Frage: „Wie ähnlich ist ein Zustand sich selbst?“ gerne eine Eins als Antwort bekommen würde.

Wenn die Zahl Null bei dieser Art von Multiplikation (man nennt es ein Inneres Produkt) herauskommt, dann bedeutet das: Die beiden Zustände sind so verschieden, wie sie nur sein könnten. Und das wiederum bedeutet nichts weiter als: Man kann sie durch eine einfache Beobachtung voneinander unterscheiden.

Das ist auch gleich die Definition dieser Art von Multiplikation. Wir haben ja für unseren Würfel festgelegt, dass Rot, Grün und Blau die drei Zustände sind, die wir ganz klar voneinander unterscheiden können. Also können wir – ganz formal und mathematisch schreiben:

Und das bedeutet einfach: Diese Zustände haben nichts miteinander zu tun – wenn der Würfel Rot ist, dann ist er nicht Grün usw.

Wenn zwei Zustände dieselben sind (also: so ähnlich, wie nur möglich), dann möchte man, wie gesagt, immer eine Eins als Ergebnis haben. Für unsere drei Zustände gilt also:

Aber dasselbe sollte eigentlich für alle Zustände gelten, denn jeder beliebige Zustand ist sich selbst so ähnlich, wie nur möglich: Die Länge jedes beliebigen Zustands sollte also auch Eins sein. Ist das einmal nicht der Fall und man hat einen Zustand, der zu lang oder zu kurz ist, muss man ihn einfach mit der richtigen Zahl multiplizieren, um ihn zu „stutzen“.

Und mit den wenigen Rechenregeln, die wir bis jetzt aufgestellt haben, können wir das sgoar jetzt schon einmal ausprobieren, man glaubt es kaum!

Dafür suchen wir uns einen beliebigen anderen Zustand und berechnen seine Länge. Nehmen wir dafür den Zustand Rot plus Blau, und nennen ihn Z:

Ein ganz normaler Zustand, dieser Z. Unser Quantenwürfel könnte also eines Tages im Zustand Z vor uns auftauchen. Was dann passiert, kommt weiter unten! Jetzt schauen wir aber erst einmal, ob die Länge dieses Zustands auch wirklich Eins ist! Wir multiplizieren ihn dafür einfach mit seinem bra (und ziehen am Ende dann noch die Wurzel):

Ausmultiplizieren – wie in der Schule – bringt zuerst:

Und von diesen bra-kets kennen wir die Länge bereits – das Ergebnis ist also:

Hier sollte doch eigentlich eine Eins herauskommen! Der Zustand Z (Rot plus Blau) ist also, so wie wir ihn aufgeschrieben haben, zu lang – und daher kein guter Zustand, um damit weiterzurechnen. Wir müssen ihn erst durch die richtige Zahl dividieren! Und was ist die richtige Zahl? Zwei? Nein! Denn nicht vergessen, die Zahl, die bei der Multiplikation eines bras mit seinem ket herauskommt, ist nicht die Länge, sondern das Quadrat der Länge. Man muss immer erst die Wurzel ziehen, um die richtige Länge zu erhalten!

Unser Ursprungszustand, Rot plus Blau, war also um die Wurzel aus zwei zu lang, also dividieren wir Rot plus Blau einfach durch die Wurzel aus zwei und nennen dann das unsere neuen, guten Zustand Z (und vergessen, dass wir den anderen Zustand auch schon Z genannt haben)!

Jetzt können wir aber auch noch die Frage stellen: Wie ähnlich sind sich die Zustände Rot und unser neuer Zustand Z? Und genau diese Frage bringt uns zum springenden Punkt: Was sehen wir, wenn wir einen Quantenwürfel betrachten, der im Zustand Z ist, aber der uns immer nur Rot, Grün oder Blau sein wird, wenn wir hinschauen?

Zuerst einmal rechnen wir dafür aus, wie ähnlich sich Rot und Z sind – dafür stecken wir Rot und Z in ein bra-ket:

Und weiter gehts! Wir schreiben als nächstes einfach aus, was Z ist – nämlich Rot plus Blau, dividiert durch die Wurzel aus zwei. Allerdings in Klammern, um nicht durcheinander zu kommen:

Denn der neue Zustand Z ist ja nichts anderes als Rot plus Blau! Dann wieder ausmultiplizieren und die Regeln von oben anwenden, die Wurzel aus Zwei können wir dabei wie eine ganz normale Zahl verwenden (ist sie ja auch) und einfach „herausheben„. Für den Rest schauen wir einfach wieder in unsere Tabelle von oben:

Die Ähnlichkeit zwischen unserem neuen Zustand Z und dem Zustand Rot ist also die Wurzel aus .

Z ist also ganz klar nicht ganz dasselbe wie Rot und nicht ganz dasselbe wie Blau, aber ein bisschen Ähnlichkeit gibt es wohl. (Z hat allerdings gar nichts mit Grün zu tun. Das kannst du mittlerweile selbst nachrechnen!).

Was bedeutet das jetzt für unseren Quantenwürfel, der im Zustand Z ist, wenn wir hinschauen? Sehen wir dann Blau oder Rot? Zur Erinnerung: den Zustand Z können wir ja nicht sehen, wir haben ja genau drei sichtbare Zustände festgelegt! Die Antwort ist einfach – und sie ist das Herz der Quantenphysik:

Wir nehmen die Zahl, die bei der bra-ket Rechnung herauskommt, quadrieren sie, und erhalten die Wahrscheinlichkeit, dass wir den Würfel, der im Zustand Z ist, als einen Roten Würfel sehen! Die Zahl war , und ihr Quadrat ist:

Mit einer Wahrscheinlichkeit von , also 50%, werden wir den Quantenwürfel Rot sehen – obwohl er eigentlich im Zustand Z (also Rot plus Blau) war! Dieselbe Rechnung lässt sich auch für die Wahrscheinlichkeit, dass wir Blau oder Grün sehen werden, anstellen – für Blau ist sie ebenfalls 50%, für Grün ist sie 0. Formal ausgedrückt:

Diese Formeln kann man so lesen: Wenn mein Würfel im Zustand Z ist (und der ist Rot plus Blau dividiert durch die Wurzel aus Zwei), ist die Wahrscheinlichkeit Rot zu sehen 50%, die Wahrscheinlichkeit Grün zu sehen 0% und die Wahrscheinlichkeit Blau zu sehen ebenfalls 50%. Und genau das ist die Stelle, an der diese vielen Wahrscheinlichkeiten in die Quantenphysik kommen – alles nur wegen den seltsamen Quantenzuständen!

Aber so schwer war das jetzt wirklich nicht, oder?

PS. Ein paar Begriffe vielleicht noch:
Wenn die Zustände alle die Länge eins haben, sind sie normiert.
Den Zustand Rot plus Blau kann man als Superposition der Zustände Rot und Blau bezeichnen.
Die Zahl, die bei der Multiplikation eines bras mit einem ket herauskommt, nennt man Wahrscheinlichkeitsamplitude – Quadriert ist sie die Wahrscheinlichkeit, zieht man ihre Wurzel, erhält man ein Maß für die Ähnlichkeit des jeweiligen bras und des kets. Die Wahrscheinlichkeitsamplitude selbst kann auch eine komplexe Zahl sein – man muss deshalb eine spezielle Form des Quadrierens verwenden, wenn man eine reale Wahrscheinlichkeit herausbekommen will.

PPS. Es gibt noch viele andere Regeln – das ist allerdings sicherlich mehrere Einträge wert.

PPPS. Mögliche quantenphysikalische Zustände lassen sich zwar nicht in einen Sack der Mengenlehre packen, aber man kann sie in einen Raum stecken: einen sogenannten Linearen Vektorraum. Keine Sorge, auch Hilberträume (nicht Träume) und Fock-Räume gibt es.